Assignment 7
Problems
Partial Differential Equations
Partial derivatives are the language in which much of modern science is written. We saw in the last portion of the course that vector valued differential equations are the right language to describe the motion of single particles: but what about quantites that depend on more than one variable?
A first example is simply waves on a string: when a guitar string is pulled taught, if you try to pluck it away from rest it pulls back on you - the farther you pull it away, the harder it pulls back. The amount a string curves away from its straight line equilibrium is captured (roughly) by its concavity. And so one simple model of string motion would say the bigger the concavity the faster it wants to “snap back”. Said more precisely
The acceleration of the string is proportional to its concavity
Writing this in math - if the string’s displacement at position \(x\) and time \(t\) is given by the function \(W(x,t)\), we have the partial differential equation below: \[\partial_{xx} W = \partial_{tt}W\]
A solution to a partial differential equation is a function \(W(x,t)\) which makes the equation true (much like a solution to an algebra equation like \(x^2=4\) is a number that makes it true, like \(x=2\).)
- Verify that the function \(W(x,t)=\sin(x-t)\) is a solution to the wave equation with a calculation. Now graph it in Desmos (using \(t\) as a parameter with a slider). Describe what the solution looks like in a sentence.
- The function \(W(x,t)=\sin(x-2t)\) does not satisfy the wave equation. Can you modify the wave equation to by multiply one of the sides by a constant to get a new partial differential equation that this does satisfy?
Tangents and Normals to Surfaces
You are working with a real-estate developer to plan new environmentally-friendly infrastructure for a community in the rolling hills of Marin county. One particular hill you are developing is well approximated by the graph of the quadratic function \[z=5-\frac{x^2}{4}-\frac{y^2}{8}\] For \((x,y)\in [-2,2]\times[-2,2]\).
Your job is to find the optimal placement along the hill for the collection of solar panels that will provide electricity for the development. Solar panels work best when the sun light shines directly perpendicularly onto their surface, so you are looking for the location on the hill where the sun hits it most perpendicularly.
Consulting a local meteorologist you learn the direction of the average noontime sun at your build site is \(\langle 1,0,-4\rangle\). At which point \((x,y,z)\) should we build the solar panel farm? To figure this out, follow the outline below.
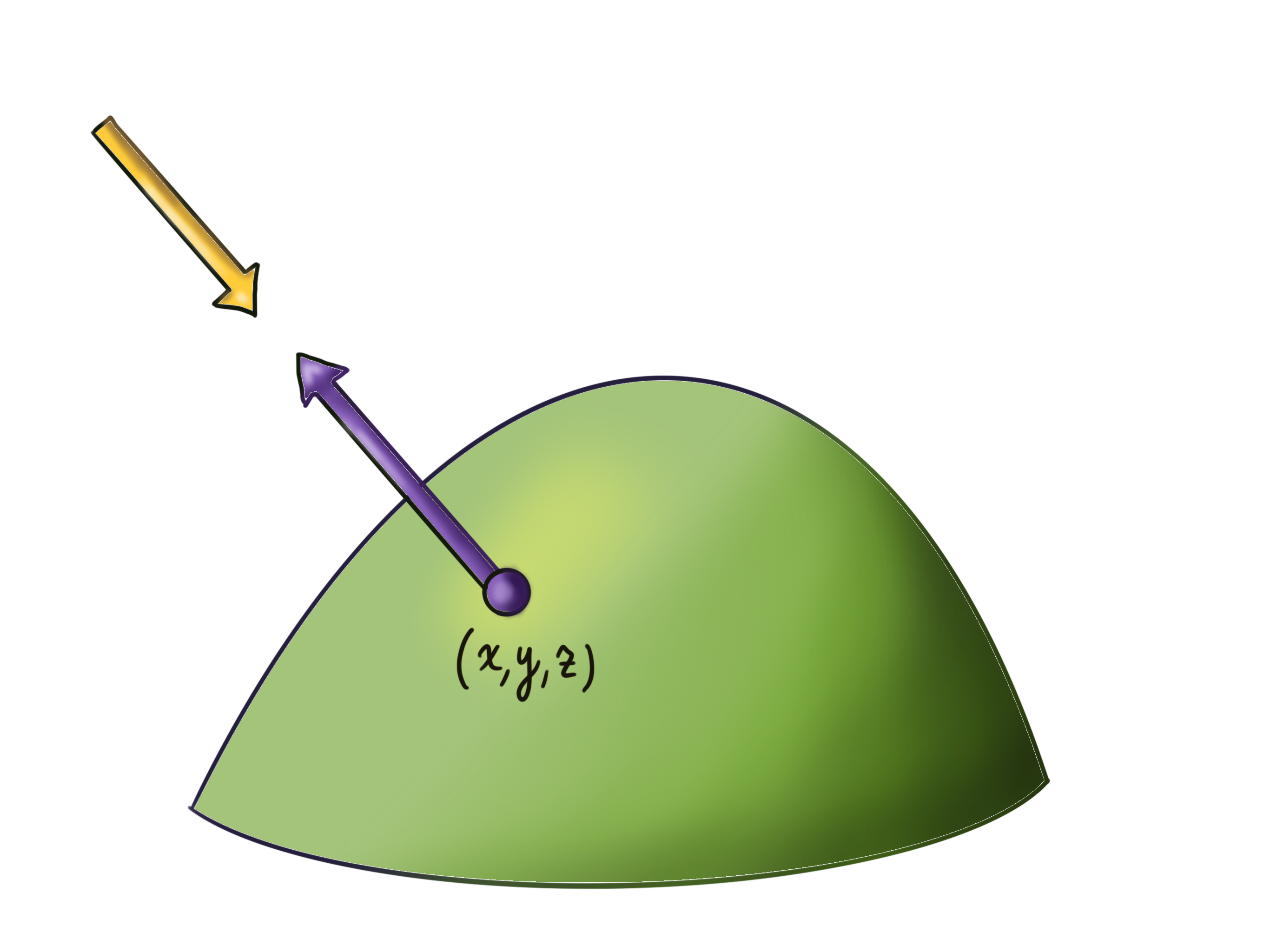
- At any point \((x,y)\) on the plane, can you use partial derivatives to find a vector which is perpendicular to the hill at that point?
- Think about the vector you found: is it pointed upwards (towards the sky) or downwards (into the hill)? There are always two directions a normal vector can point, and either one is fine but its important to know which one you are working with in applications.
- Our real goal is to find when the hill is perpendicular to the direction of the sun. For which \((x,y)\) is the vector you found parallel (or, anti-parallel) to this?
Linear and Quadratic Approximations to Surfaces
Recall in Calculus I that a critical point of a function \(f\) is a point where the derivative is zero. Such critical points come up when trying to optimize a function (find a maximum or minimum value), but you may remember that more information is needed: we use something like the second derivative test to help us distinguish between maxima, minima, and other things like inflection points. A similar story plays out in multiple variables, and we will build it up in class shortly. In this problem we will just get a quick preview.
Imagine you are once again working for an engineering firm from last week’s assignment, where your team is tasked with maximizing the efficiency \(E\) of a rocket engine by varying the nozzle size \(n\) and the fuel temperature \(t\). The physics of the problem are too difficult to write down an equation for \(E\) by hand, so instead you have to resort to asking a computer to fun a simulation. Your simulation is able to compute the value of \(E\) and its derivatives at different inputs. Here are two example outputs from the program:
The Point \((n,t)=(1,2)\) \[E(1,2)=3,\, E_n(1,2)=1,\, E_t(1,2)=0\] \[ E_{nn}(1,2)=4,\, E_{tn}(1,2)=3,\, E_{nt}(1,2)=3,\, E_{tt}(1,2)=0\]
The Point \((n,t)=(4,1)\) \[E(4,1)=8,\, E_n(4,1)=0,\, E_t(4,1)=0\] \[ E_{nn}(4,1)=-3,\, E_{tn}(4,1)=0,\, E_{nt}(4,1)=0,\, E_{tt}(4,1)=-5\]
Question 1: Use the first derivatives to explain why \((1,2)\) is neither a maximum or minimum of efficiency.
Question 2: At \((4,1)\) the first derivatives are zero. This means a linear approximation alone is not useful to us, so we are at a critical point. To try and figure out if it is a maximum, minimum of zero we can go beyond linear and try a quadratic approximation, the multivariable analog of a second-order Taylor series.
Write down the quadratic approximation to \(E\) based at \((4,1)\), as a function of \(n\) and \(t\). Think back to our study of quadratic surfaces: perhaps by looking at slices of this (perhaps at \(n=4\) and \(t=1\)?), can you tell if its a max, min or saddle?
Solutions
Partial Differential Equations
To verify \(W(x,t)=\sin(x-t)\) solves the wave equation, we just need to differentiate with respect to both variables twice, and observe what we get are equal:
\[W=\sin(x-t)\hspace{1cm}W_x=\cos(x-t)\hspace{1cm}W_{xx}=-\sin(x-t)\] \[W=\sin(x-t)\hspace{1cm}W_t=\cos(x-t)(-1)\hspace{1cm}W_{tt}=-\sin(x-t)(-1)(-1)\] Since \((-1)^2=1\) these two are equal, so \(W\) solves the wave equation.
The second proposed \(W\) does not solve the wave equation as \[W_xx= -\sin(x-2t)\hspace{1cm}W_{tt}=-4\sin(x-2t)\] However we can see directly the second time derivative is four times the second space derivative, so an equation it does satisfy is \[W_{tt}=4W_{xx}\]
Tangents and Normals to Surfaces
In this problem we know the direction of the sun’s rays, and we want to know when the normal vector to the hill is parallel to this: that is when is the hills normal vector a scalar multiple of \(\langle 1,0,-4\rangle\)?
The first step is to find the normal vector to the hill \(z=5-\frac{x^2}{4}-\frac{y^2}{8}\) at the point \((x,y)\). In class, we found the normal vector to the graph of a multivariate function to be the coefficient vector from its tangent plane:
\[n=\langle f_x,f_y,-1 \rangle\]
This version is downward pointing as the \(z\) component is \(-1\), so looking at our picture, this normal vector is pointed into the hill.
Alternatively - if we did not remember this we could derive it using our multivariate tools of partial differentiation and the cross product! Here we could find two vectors that are tangent to the hill using partial derivatives: if you move infinitesimally one unit in the \(x\) direction your \(z=f(x,y)\) component will move by \(\partial_x f\), and so the vector \[v_x = \pmat{1\\ 0 \\ f_x}\] is tangent in the \(x\)-direction. Similarly, \(v_y=\langle 0,1 f_y\rangle\) is tangent in the \(y\) direction, and their cross product is normal: \[n=v_x\times v_y=\left| \begin{matrix}\ihat &\jhat&\khat\\ 1&0& f_x\\ 0&1& f_y \end{matrix} \right|=\pmat{-f_x \\ -f_y\\ 1}\] This normal is upward pointing at \(z\) is positive: looking at our picture its pointed out of the hill.
To find the actual vector for this problem, we need to calculate these derivatives:
\[f_x = -\frac{x}{2}\hspace{1cm}f_y=-\frac{y}{4}\] \[n=\left\langle\frac{-x}{2},\frac{-y}{4},-1\right\rangle\]
To figure out when this is a multiple of \(\langle 1,0,-4\rangle\) we are just asking when there is a single constant \(c\) such that
\[k\pmat{-x/2\\ -y/4 \\ -1}=\pmat{1\\ 0 \\ -4}\]
This is a system of three equations that we need to solve. The bottom equation tells us that \(k = 4\). Substituting this into the second equation, we see \(-ky/4 = 0\) implies \(y=0\), and into the first equation yields \[-kx/2 = -4x/2=2x=1\hspace{0.25cm}\implies\hspace{0.5cm}x=-1/2\]
Thus the point where the normal vector is parallel to the sunrays - where we should place our solar panel on the hill has \((x,y)\) coordinates \((-1/2,0)\).
Linear and Quadratic Approximations
For the first part, we notice that \(E_n(1,2)=1\), so the rate of change in the \(n\) direction is positive: that is, as we make \(n\) get bigger the efficiency grows and as we make \(n\) smaller the efficiency shrinks. Thus we couldn’t have been at either a max or a min. If we wanted to get quantitative about this, we could look at the linear approximation
\[\begin{align*} L(t,n)&=E(1,2)+E_n(1,2)(n-1)+E_t(1,2)(t-2)\\ &=3+1(n-1)+0(t-2)\\ &= 2+n \end{align*}\]
Since this is a good approximation of \(E\) when \((n,t)\approx(1,2)\), we see that around this point \(E\) kind of looks like a plane that is sloped in the \(n\) direction, whereas near a max or min we should expect it to have a horizontal tangent plane.
For the second part, \(E_n\) and \(E_t\) are both equal to zero, so the linear approximation is a horizontal tangent plane! Here we have to move to the quadratic approximation to get some information:
\[\begin{align*} Q(n,t)&=E(4,1)+E_n(4,1)(n-4)+E_t(4,1)(t-1)+\\ &+\frac{1}{2}\left(E_{nn}(4,1)(n-4)^2+E_{nt}(4,1)(n-4)(t-1)+E_{tn}(4,1)(t-1)(n-4)+E_{tt}(4,1)(t-1)^2\right)\\ &= 8+0+0+\frac{1}{2}\left(-3(n-4)^2+0+0-5(t-1)^2\right)\\ &= 8-3(n-4)^2-5(t-1)^2 \end{align*}\]
The coefficients in front of the \(n^2\) and \(t^2\) terms are negative so both the slices for constant \(n\) and constant \(t\) are downwards facing parabolas. This suggests the entire shape is a parabola shaped hill, and so the point \((4,1)\) is actually a maximum!