3 Operations

(Relevant Sections of the Textbook: 12.3 The Dot Product, and 12.4 The Cross Product)

3.1 The Dot Product

The dot product is an operation which takes in two vectors and outputs a single number. We will use it as a tool to measure several things, but it’s perhaps easiest to learn by just diving right in with the definition.

Definition 3.1 (Dot Product) If $\vec{u} = ⟨ u_{1}, u_{2}, u_{3} ⟩$ and $\vec{v} = ⟨ v_{1}, v_{2}, v_{3} ⟩$ then the dot product of $\vec{u}$ and $\vec{v}$ is the scalar $\vec{u} \cdot \vec{v} = u_{1} v_{1} + u_{2} v_{2} + u_{3} v_{3}$ And similarly in other dimensions, if $\vec{u}, \vec{v}$ are vectors in $n$ dimensions, then $\vec{u} \cdot \vec{v} = \sum_{i = 1}^{n} u_{i} v_{i}$

For example, the dot product of $⟨ 1, 2 ⟩$ and $⟨ 3, 4 ⟩$ is $1 \times 3 + 2 \times 4 = 3 + 8 = 11$ , and the dot product of $\hat{ı} - \hat{ȷ}$ and $2 \hat{ı} - \hat{ȷ} + 3 \hat{k}$ can be computed by either (1) converting to coordinate notation, or (2) pairing up coefficients and multiplying.

$(\hat{ı} - \hat{ȷ}) \cdot (2 \hat{ı} - \hat{ȷ} + 3 \hat{k}) = (1 \times 2) + (- 1 \times - 1) + (0 \times 3) = 3$

We will unpack a lot more of the geometry hidden inside of this simple defintion soon, but a first thing to notice is that the magnitude of a vector can be recovered from its dot product with itself.

Theorem 3.1 If $\vec{u}$ is any vecotr, then the magnitude of $\vec{u}$ can be calculated via $∥ \vec{u} ∥ = \sqrt{\vec{u} \cdot \vec{u}}$

Exercise 3.1 Check that this works for the vector $⟨ x, y, z ⟩$ in $R^{3}$ .

The dot product is built out of the multiplication and addition of ordinary numbers, so it also inherits alot of their algebraic properties:

Theorem 3.2 (Properties of the Dot Product) If $\vec{u}, \vec{v}$ and $\vec{w}$ are vectors and $c, k$ are scalars then

$\vec{0} \cdot \vec{u} = \vec{0} \vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{u}$

$\vec{u} \cdot (\vec{v} + \vec{w}) = \vec{u} + \vec{w} + \vec{v} \cdot \vec{w} c (\vec{u} \cdot \vec{v}) = c (\vec{u} \cdot \vec{v}) = \vec{u} \cdot (c \vec{v})$

3.1.1 Measuring Angles

We’ve already seen that the dot product of a vector with itself measures the (square of the) magnitude of that vector. But dot products are also able to recover direction information as well.

Theorem 3.3 (Angles and the Dot Product) If $\vec{u}, \vec{v}$ are vectors, their dot product is related to the angle $θ$ between them via $\vec{u} \cdot \vec{v} = | \vec{u} | | \vec{v} | \cos θ$ Re-arranging this, we get a formula that computes the angle between two vectors using only vector operations!

$\cos θ = \frac{\vec{u} \cdot \vec{v}}{| \vec{u} | | \vec{v} |}$

Exercise 3.2 What is the angle between $⟨ 1, 2 ⟩$ and $⟩ 3, 4 ⟩$ in radians?

What is the angle between $\hat{ı} + \hat{ȷ}$ and $\hat{ȷ}$ in degrees?

Definition 3.2 (Orthogonality) Two vectors are called orthogonal if the angle between them is 90 degrees, or $π / 2$ radians. Since $\cos (π / 2) = 0$ , this means that two vectors are orthogonal if and only their dot product is zero.

Note that the zero vector dotted with any other vector always gives zero, so we say the zero vector is orthogonal to every other vector.

3.1.2 Projections

One very useful application of the dot product is to help measure “how much of vector $\vec{v}$ is pointed in direction $\hat{u}$ ?”

The scalar projection of $\vec{v}$ onto the unit vector $\hat{u}$ is the dot product $\vec{v} \cdot \hat{u}$ . If $\vec{u}$ is not a unit vector to start with, we first make it into a unit vector by dividing by its magnitude, to find the scalar projection: $ $\vec{v} \cdot \hat{u} = \vec{v} \cdot \frac{\vec{u}}{| \vec{u} |}$

Definition 3.3 (Scalar Projection) The scalar projection of $\vec{v}$ onto $\vec{u}$ is ${comp}_{\vec{u}} (\vec{v}) = \frac{\vec{v} \cdot \vec{u}}{| \vec{u} |}$

Exercise 3.3 (Scalar Projection) What is the scalar projection of $⟨ 1, 2 ⟩$ onto $⟨ 3, 4 ⟩$ ?

What is the scalar projection of $⟨ 4, 3, - 2 ⟩$ onto $⟨ 0, 1, 0 ⟩$ ?

This tells us how much of a vector is pointed in a given direction, and so the answer is a scalar, or number. Oftentimes it is useful to compute a vector from this, whose direction is in the direction of $\vec{u}$ , and magnitude is the scalar we just computed. This vector can be thought of as the projection of $\vec{v}$ onto $\vec{u}$ , or the shadow of $\vec{v}$ on the line spanned by $\vec{u}$ .

PICTURE

Definition 3.4 (Vector Projection) The vector projection of a vector $\vec{v}$ onto a vector $\vec{u}$ is the scalar projection times the *unit vector in direction $\vec{u}$ . In symbols:

$\begin{aligned} {proj}_{\vec{u}} (\vec{v}) & = {comp}_{\vec{u}} (\vec{v}) \\ = (\frac{\vec{v} \cdot \vec{u}}{∥ \vec{u} ∥}) \frac{\vec{u}}{∥ \vec{u} ∥} \\ = \frac{\vec{v} \cdot \vec{u}}{\vec{u} \cdot \vec{u}} \vec{u} \end{aligned}$

Exercise 3.4 (Vector Projection) Find the vector projection of $⟨ 1, 1, 2 ⟩$ onto the vector $⟨ - 2, 3, 1 ⟩$ .

3.1.3 Standard Basis

Theorem 3.4 If $\vec{v} = ⟨ a, b, c ⟩$ is a vector, its scalar projections onto the three standard basis vectors $\hat{ı}, \hat{ȷ}, \hat{k}$ are ${comp}_{\hat{ı}} (\vec{v}) = \vec{v} \cdot \hat{ı} = a$ ${comp}_{\hat{ȷ}} (\vec{v}) = \vec{v} \cdot \hat{ȷ} = b$ ${comp}_{\hat{k}} (\vec{v}) = \vec{v} \cdot \hat{k} = c$

This confirms our notions of “amount” and “angle” make sense with our original interpretation of the vector $⟨ a, b, c ⟩$ as being an amount $a$ in the direction $\hat{ı}$ , $b$ in the direction $\hat{ȷ}$ , and $c$ in the direction $\hat{k}$ .

Theorem 3.5 (Direction Angle) The angles $α, β, γ$ a vector $\vec{v} = ⟨ a, b, c ⟩$ makes with the direction of the standard basis $\hat{ı}, \hat{ȷ}, \hat{k}$ respectively are $\cos α = \frac{\vec{v} \cdot \hat{ı}}{∥ \vec{v} ∥} = \frac{a}{∥ \vec{v} ∥}$ $\cos β = \frac{\vec{v} \cdot \hat{ȷ}}{∥ \vec{v} ∥} = \frac{b}{∥ \vec{v} ∥}$ $\cos γ = \frac{\vec{v} \cdot \hat{k}}{∥ \vec{v} ∥} = \frac{c}{∥ \vec{v} ∥}$

3.2 Cross Product

In two dimensions, given one vector $\vec{v} = ⟨ a, b ⟩$ it is easy to find an orthogonal vector to it: ${\vec{v}}^{⊥} = ⟨ b, - a ⟩$ for example.

In 3D, the analogous problem is more difficult: given two vectors, how do we find a third vector that is orthgonal to them both at once? A nice solution to this is given by the cross product.

Definition 3.5 (Cross Product) The cross product of $\vec{u} = ⟨ u_{x}, u_{y}, u_{z} ⟩$ and $\vec{v} = ⟨ v_{x}, v_{y}, v_{z} ⟩$ is $\vec{u} \times \vec{v} = ⟨ u_{y} v_{z} - u_{z} v_{y}, u_{x} v_{z} - u_{z} v_{x}, u_{x} v_{y} - u_{y} v_{x} ⟩$

Open Fullscreen

Exercise 3.5 (Orthogonality of the Cross Product) Check that if $\vec{u} = ⟨ a, b, c ⟩$ and $\vec{v} = ⟨ x, y, z ⟩$ are two vectors, that $\vec{u} \times \vec{v}$ is orthogonal to both $\vec{u}$ and $\vec{v}$ .

While there are many vectors orthogonal to $\vec{u}$ and $\vec{v}$ , this particular choice has some very nice mathematical properties. In particular, it gets it’s name because it acts algebraically a lot multiplication:

Theorem 3.6 (Properties of the Cross Product) Let $\vec{u}, \vec{v}, \vec{w}$ be vectors, and $k$ a scalar. Then $\vec{u} \times (\vec{v} + \vec{w}) = \vec{u} \times \vec{v} + \vec{u} \times \vec{w}$ $(\vec{u} + \vec{v}) \times \vec{w} = \vec{u} \times \vec{w} + \vec{v} \times \vec{w}$ $(k \vec{u}) \times v = k (\vec{u} \times \vec{v}) = \vec{u} \times (k \vec{v})$

However, the cross product has two very important differences from regular multiplication: the order matters!

Theorem 3.7 (Non-Commutativity of the Cross Product) If $\vec{u}$ and $\vec{v}$ are vectors, then $\vec{u} \times \vec{v} = - \vec{v} \times \vec{u}$

Not only does the order that you place the vectors in the product matter, but if you are doing more than one cross product, the order in which you perform them matters as well!

Theorem 3.8 (Non-Associativity of the Cross Product) If $\vec{u}$ , $\vec{v}$ and $\vec{w}$ are vectors, then $(\vec{u} \times \vec{v}) \times \vec{w} \neq \vec{u} \times (\vec{v} \times \vec{w})$

3.2.1 Computing the Cross Product

Definition 3.6 ( $2 \times 2$ determinants) The determinant of a $2 \times 2$ matrix is $| \begin{matrix} a & b \\ c & d \end{matrix} | = a d - b c$

Using this notation, we can recast the definition of the cross product from Definition 3.5 to look like

$\vec{u} \times \vec{v} = | \begin{matrix} u_{y} & u_{z} \\ v_{y} & v_{z} \end{matrix} | \hat{ı} - | \begin{matrix} u_{x} & u_{z} \\ v_{x} & v_{z} \end{matrix} | \hat{ȷ} + | \begin{matrix} u_{x} & u_{y} \\ v_{x} & v_{y} \end{matrix} | \hat{k}$

Note the minus sign on the second term (compare with Definition 3.5 to see where a $- 1$ was factored out). This formula can in turn be written even more compactly using the definition of a $3 \times 3$ determinant:

Definition 3.7 ( $3 \times 3$ determinants) The determinant of a $3 \times 3$ matrix is $| \begin{matrix} x & y & z \\ a & b & c \\ d & e & f \end{matrix} | = x | \begin{matrix} b & c \\ e & f \end{matrix} | - y | \begin{matrix} a & c \\ d & f \end{matrix} | + z | \begin{matrix} a & b \\ d & e \end{matrix} |$

Putting it all together,

Definition 3.8 The cross product of $\vec{u} = ⟨ u_{x}, u_{y}, u_{z} ⟩$ and $\vec{v} = ⟨ v_{x}, v_{y}, v_{z} ⟩$ is $\begin{aligned} \vec{u} \times \vec{v} & = | \begin{array}{c} \hat{ı} & \hat{ȷ} & \hat{k} \\ u_{x} & u_{y} & u_{z} \\ v_{x} & v_{y} & v_{z} \end{array} | \\ = | \begin{array}{c} u_{y} & u_{z} \\ v_{y} & v_{z} \end{array} | \hat{ı} - | \begin{array}{c} u_{x} & u_{z} \\ v_{x} & v_{z} \end{array} | \hat{ȷ} + | \begin{array}{c} u_{x} & u_{y} \\ v_{x} & v_{y} \end{array} | \hat{k} \end{aligned}$

While the cross product is specific to three dimensions, later in the course we will sometimes apply it to 2-dimensional vectors, where we think of a vector $\vec{v} = ⟨ x, y ⟩$ in $R^{2}$ as being the vector $\vec{v} = ⟨ x, y, 0 ⟩$ in $R^{3}$ . In this case, the cross product of two planar vectors has a rather simple formula (for instance, we know it must point directly along the $z$ -axis!)

Definition 3.9 (Planar Cross Product) If $\vec{u} = ⟨ a, b ⟩$ and $\vec{v} = ⟨ c, d ⟩$ are two vectors in $R^{2}$ , their cross product, when thought of as vectors in the $x y$ plane of $R^{3}$ is $\vec{u} \times \vec{v} = | \begin{matrix} a & b \\ c & d \end{matrix} | \hat{k} = ⟨ 0, 0, a d - b c ⟩$

3.2.2 Geometry of the Cross Product

The main property of the cross product is that it’s a third vector that its orthogonal to the two vectors you start with. If you did Exercise 3.5, you’ve already proven this theorem:

Theorem 3.9 (Orthogonality of the Cross Product) The vector $\vec{u} \times \vec{v}$ is orthogonal to both $\vec{u}$ and $\vec{v}$ .

Howver there is an entire line of vectors orthogonal to $\vec{u}$ and $\vec{v}$ . Which of these is the cross product? We need to understand its magnitude and its direction.

Theorem 3.10 The magnitude of the cross product $\vec{u} \times \vec{v}$ is given in terms of the magnitudes of $\vec{u}$ and $\vec{v}$ , and the angle $θ$ between them: $| \vec{u} \times \vec{v} | = | \vec{u} | | \vec{v} | \sin θ$

This formula, base times height times the sine of the angle between them may be familiar as the area of a parallelogram. That gives an even more useful interpretation of the cross product’s length:

Theorem 3.11 The magnitude of the cross product $\vec{u} \times \vec{v}$ is the area of the parallelogram spanned by $\vec{u}$ and $\vec{v}$ .

This has an immediate corollary: if $\vec{u}$ and $\vec{v}$ are parallel the parallelogram they span collapses onto a line. And lines have zero area, so the cross product must have zero length! That is, it must be the vector of all zeroes.

Corollary 3.1 If $\vec{u}$ and $\vec{v}$ are parallel, then their cross product is the zero vector.

This gives us the magnitude information, but what about the direction? There are two possible directions a vector could point if it must be perpendicular to the plane containing $\vec{u}$ and $\vec{v}$

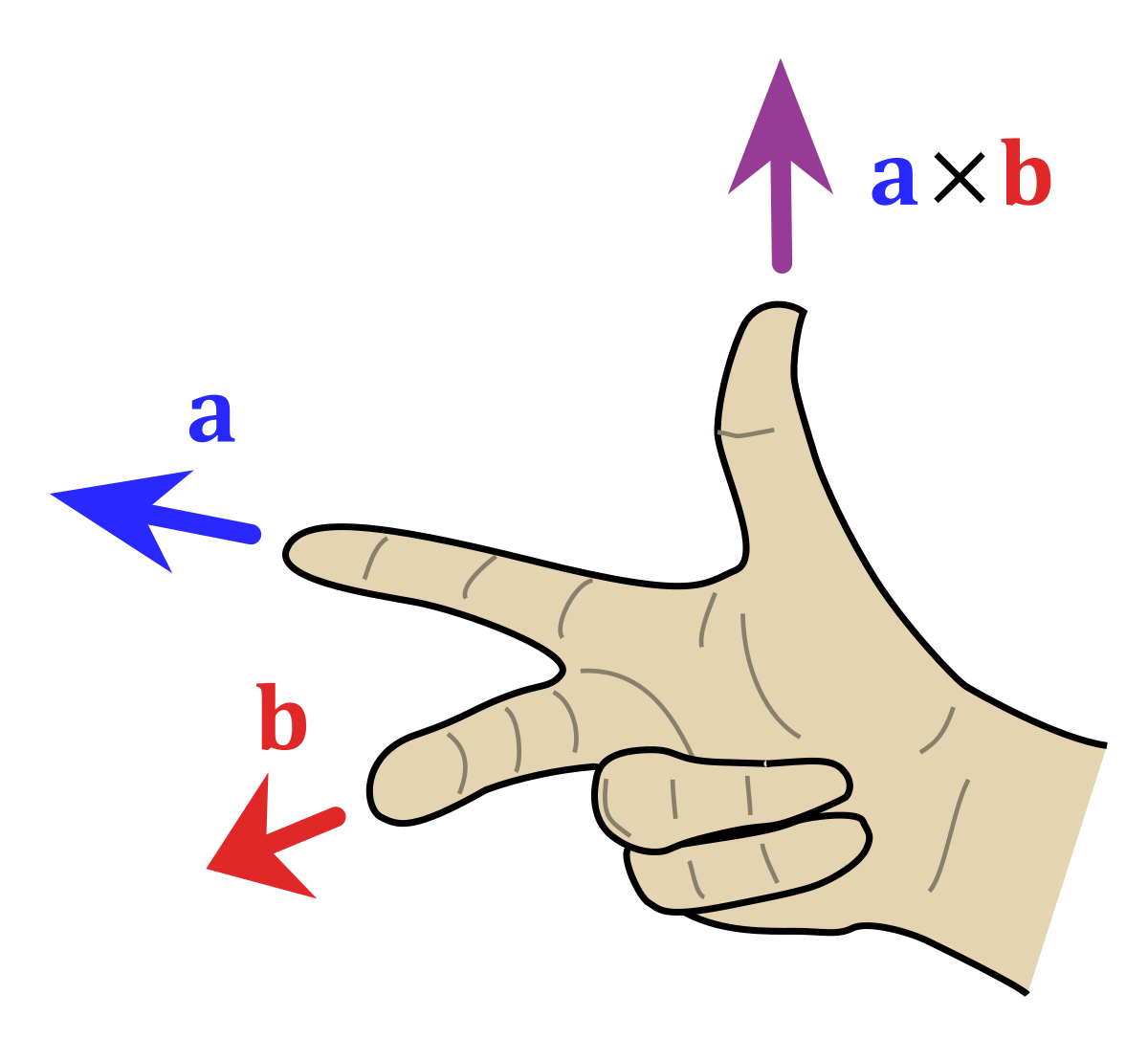
Theorem 3.12 (The Right Hand Rule) The right hand rule is a mnemonic to help remember the direction of the cross product. If you take your right hand and align your palm with the vector $\vec{u}$ and then curl your fingers towards the vector $\vec{v}$ , your thumb will point in the direction $\vec{u} \times \vec{v}$ .

3.2.3 The Standard Basis

It’s often useful to know the value of the cross product on the standard basis vectors, to speed up some computations and avoid the lengthy formula in Definition 3.8.

Theorem 3.13 $\begin{matrix} \hat{ı} \times \hat{ȷ} = \hat{k} & \hat{ȷ} \times \hat{k} = \hat{ı} & \hat{k} \times \hat{ı} = \hat{ȷ} \end{matrix}$

This is helpfully illustrated by a diagram:

Recalling that the cross product changes sign when you reverse the order of the inputs, its possible to compute the rest of the possible stanard basis products: $\hat{ı} \times \hat{ȷ} = \hat{k} ⟹ \hat{ȷ} \times \hat{ı} = - \hat{k}$

In terms of the diagram, this means if you read “backward” along an arrow, you insert a minus sign.

3.3 The Triple Product

If you have three vectors, its possible to combine the dot and cross product to get a single number: take the cross product of two of them to get another vector, then dot that result with the third.

Definition 3.10 (Triple Product) The scalar triple product of the vectors $\vec{u}, \vec{v}$ and $\vec{w}$ is defined by $\vec{u} \cdot (\vec{v} \times \vec{w})$

Writing out the cross product using Definition 3.8, we see that this is actually a big $3 \times 3$ determinant:

Theorem 3.14 (Triple Product) The triple product of vectors $\vec{u}, \vec{v}, \vec{w}$ is equal to the $3 \times 3$ determinant $\vec{u} \cdot (\vec{v} \times \vec{w}) = | \begin{matrix} u_{x} & u_{y} & u_{z} \\ v_{x} & v_{y} & v_{z} \\ w_{x} & w_{y} & w_{z} \end{matrix} |$

Just as the $2 \times 2$ determinant measures the area of a parallelogram, this $3 \times 3$ determinant measures the volume of a parallelpiped

Theorem 3.15 (Triple Products & Volume) The magnitude of the triple product of $\vec{u}, \vec{v}, \vec{w}$ is the volume of the parallepiped spanned by these vectors.