$$ \newcommand{\RR}{\mathbb{R}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\CC}{\mathbb{C}} \newcommand{\NN}{\mathbb{N}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\EE}{\mathbb{E}} \newcommand{\HH}{\mathbb{H}} \newcommand{\SO}{\operatorname{SO}} \newcommand{\dist}{\operatorname{dist}} \newcommand{\length}{\operatorname{length}} \newcommand{\uppersum}[1]{{\textstyle\sum^+_{#1}}} \newcommand{\lowersum}[1]{{\textstyle\sum^-_{#1}}} \newcommand{\upperint}[1]{{\textstyle\smallint^+_{#1}}} \newcommand{\lowerint}[1]{{\textstyle\smallint^-_{#1}}} \newcommand{\rsum}[1]{{\textstyle\sum_{#1}}} \newcommand{\partitions}[1]{\mathcal{P}_{#1}} \newcommand{\erf}{\operatorname{erf}} \newcommand{\ihat}{\hat{\imath}} \newcommand{\jhat}{\hat{\jmath}} \newcommand{\khat}{\hat{k}} \newcommand{\pmat}[1]{\begin{pmatrix}#1\end{pmatrix}} \newcommand{\smat}[1]{\left(\begin{smallmatrix}#1\end{smallmatrix}\right)} $$

17  Integrals & Coordinates

We’ve seen previously that certain double and triple integrals are particularly challenging because their bounds contain complicated expressions like \(\sqrt{1-x^2}\), which lead to you having to do an integral of functions containing things like \(\sqrt{1-x^2}\) which leads to difficult trigonometric substitutions, or worse.

These sort of expressions come up when integrating over circular, cylindrical and spherical regions, because these are all described with equations like \(x^2+y^2=1\) or \(x^2+y^2+z^2=1\) in \(\RR^2\) or \(\RR^3\). And this chapter is the bearer of good news: the reason these integrals look hard at first is that the cartesian coordinates \(x,y,z\) are not a good way to work with them. But, after adapting our viewpoint, all the square roots melt away and these integrals become straightforward to compute!

The reason is that cartesian coordinates are good for describing flat objects: the surfaces where one variable is held constant describe lines or planes. Thus, integrals over rectangles and boxes are easy in cartesian coordinates: their bounds are constants! To make integrals over circles, cylinders and spheres easy, we need to find coordinates for which circles, cylinders and spheres are described by constants. If we can change our perspective to work with these coordinates, we will be able to turn an integral with difficult bounds into a different integral with constant bounds - but the same overall value.

17.1 Polar Coordinates

Polar coordinates are a means of representing the plane using distance \(r\) from the origin, and angle \(\theta\) from the \(x\)-axis.

Polar Coordinates definition.

Using trigonometry, we can relate these to the usual \(x\) and \(y\) coordinates we are used to.

Definition 17.1 (Polar Coordinates) Polar coordinates on the plane are the coordinates \(r,\theta\) where \(r\) measures the distance from the origin, and \(\theta\) measures the angle from the \(x-\)axis. The conversion from cartesian to polar coordinates is given by the functions

\[x=r\cos\theta \hspace{1cm}y=r\sin\theta\]

Definition 17.2 (dA in Polar Coordinates) \[dA=rdrd\theta\]

This lets us do a double integral in polar coordinates by first doing an \(r\) integral, and then a \(\theta\) integral or vice-versa:

\[\iint_R f\, dA = \int_{\theta_1}^{\theta_2}\int_{r_1}^{r_2}f\,rdrd\theta\]

Just like in cartesian coordinates, you can view this as slicing in teh \(r\) and \(\theta\) directions, and integrating the results.

Open Fullscreen

Starting from an integral with cartesian coordinates \(x,y\), there is a straightforward procedure to convert to polar:

  • Convert the function to polar coordinates: substitute \(x=r\cos\theta\) and \(y=r\sin\theta\) and simplify (remember \(x^2+y^2=r^2\)).
  • Substitute \(dA\) or \(dxdy\) for the polar area unit \(dA=rdrd\theta\).
  • Rewrite the bounds of integration in terms of polar coordinates.

Now you just have a standard iterated integral (but with variables named \(r\) and \(\theta\) instead of \(x\) and$ y$.) This can be computed as normal: just doing one integral at a time.

Example 17.1  

17.2 Cylindrical Coordinates

Cylindrical coordinates are just the natural three dimensional extension of polar coordinates, where we use \(r,\theta,\) and \(z\).

Cylindrical coordinates definition

Definition 17.3 (Cylindrical Coordinates) Measure two directions in space using polar coordinates, and the orthogonal direction with its standard Cartesian axis. If we convert the \(xy\) plane to polar, this means

\[x=r\cos\theta\] \[y=r\sin\theta\] \[z=z\]

The volume element here is just the polar area element times \(dz\):

Definition 17.4 (Volume in Cylindrical Coordinates) \[dV=(dA)dz=rdrd\theta dz\]

I’ve recorded example videos of this, for our asynchronous lecture day! The video links are available on canvas.

17.3 Spherical Coordinates

Spherical coordinates is a coordinate system in \(\RR^3\) where we represent a point with latitude, longitude, and radius.

Defining spherical coordinates.

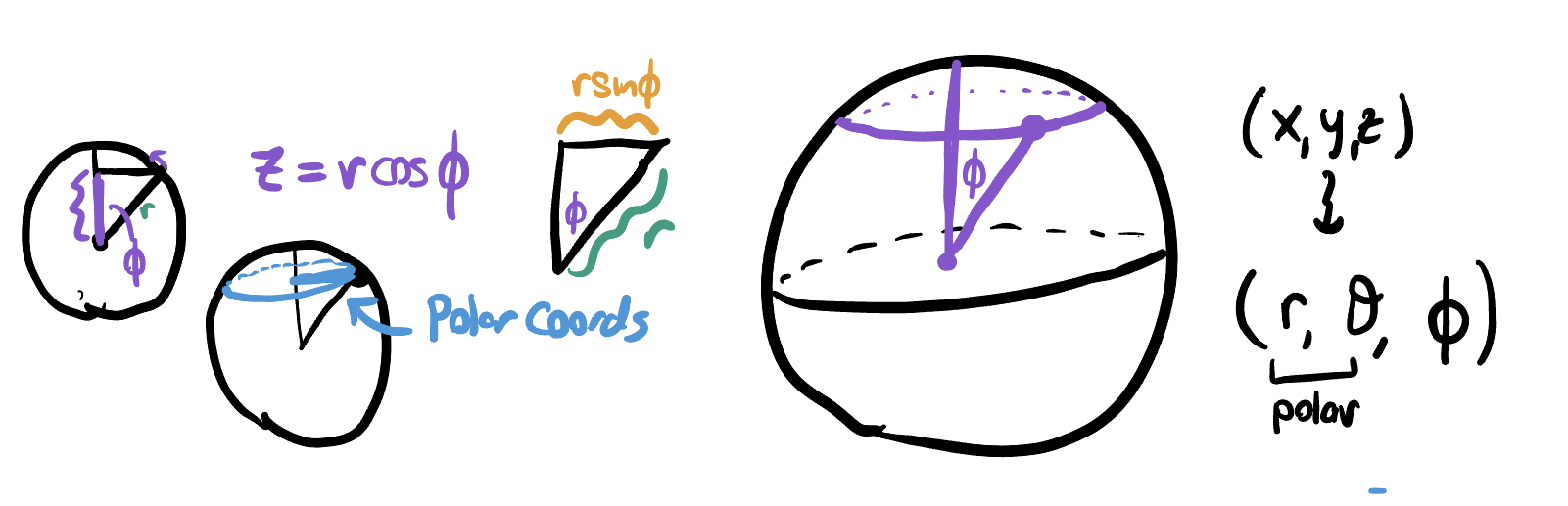
Definition 17.5 (Spherical Coordinates) \[x=r\cos\theta\sin\phi\] \[y=r\sin\theta\sin\phi\] \[z=r\sin\phi\]

Using these coordinate definitions we can compute the volume element in spherical coordinates: it’ll be a product of the length in the \(r\) direction, the length in the \(\theta\) direction and the length in the \(\phi\) direction.

  • Length in the \(r\) direction is \(dr\).
  • Circles in the \(\theta\) direction (lines of longitude) have circumference \(2\pi r \sin\phi\). Thus a small amount of angle has length \(r\sin\phi d\theta\).
  • Circles in the \(\phi\) direction are all longitudes on the sphere, of length \(2\pi r\). Thus a small bit of angle has length \(r d\phi\).

Definition 17.6 (Volume in Spherical Coordinates) \[dV=dr (r\sin\phi d\theta)(r d\phi)\] \[=r^2\sin\phi dr d\theta d\phi\]

Surfaces of \(r,\theta,\phi\) = constant.

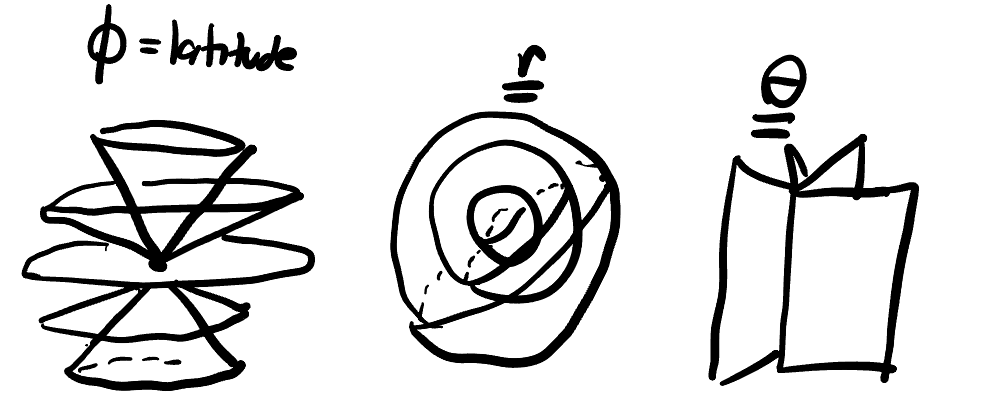
For examples of doing integrals in spherical coordinates, I recorded videos and posted them to our course Canvas page for the asynchronous lecture.

17.4 Video Resources